(writing in progress)
I bit the bullet – I am going to dig into Scribus, and add it to my toolkit.
http://www.scribus.net/downloads/
Adobe is not what it used to be. The company becomes increasingly erratic and difficult to work with for a third-party developer. As far as I can tell, Adobe is ‘doing a Quark’ on a large subset of its users.
So, after ten years of neglecting it, I’m getting back up to speed on automation with QuarkXPress 2015, and I am also looking at Scribus.
I looked at Scribus a while back and did not get very far before I lost interest. As far as I could tell, Scribus was nowhere near as powerful as InDesign, so it would not be an option for many people.
This time around I decided to look mainly at what it can do, rather than concentrate on what it cannot do. Scribus will only improve if more people start using it; it’s a chicken-and-egg situation.
I want to make sure I can help automate projects where Scribus is an option. And Scribus is definitely powerful enough to be useful for a range of real-life projects.
Getting into Scribus
Getting into Scribus will be different for everyone.
I’m looking for things that I’m familiar with. As I go, I try to map things I know from other environments onto things I discover in Scribus.
I just spent half an hour with Scribus and its documentation, and as far as I can tell, the available documentation is not a good resource for the kinds of questions I have as an system designer and automator.
What I intend to do here is keep track of my questions and the answers I found.
Anyone else in the automation game is bound to have similar questions and might find my notes useful.
I’ll be using a Mac most of the time, but I’ll also take sneak peeks at the Windows and Linux versions along the way.
I’ll be looking at both Scribus 1.4.5 and Scribus 1.5.0. According to the web page, 1.4.x is a stable version, whereas 1.5.x is a development version.
1.5.x has some interesting things in its feature list, like IDML import. I’ll be trying that out!
What about scripts?
Being in automation, this is an important point for me.
Scribus can be scripted, and the ‘native’ scripting language is Python, rather than ExtendScript. That’s cool.
Ok, let’s try to do a few ‘Hello World’ scenarios and see if we learn anything.
First, I did a bit of snooping, stole some sample code left and right, and came up with the following script:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import sys
import scribus
scribus.messageBox('Python Version', sys.version, icon=scribus.ICON_NONE, button1=scribus.BUTTON_OK)
I saved this file to my desktop as Version.py, and then used the Script – Execute Script… menu item to run this script from Scribus 1.4.5 and 1.5.0.
From Scribus 1.4.5 on Mac OS X 10.11:
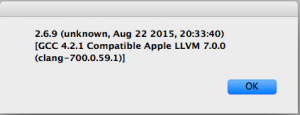
From Scribus 1.5.0 on Mac OS X 10.11:
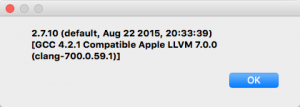
This tells me that Scribus uses Python 2.x, and that it uses an embedded Python interpreter, rather than relying on the Python interpreter provided by the Mac OS. Otherwise I would expect the two Python interpreter versions to be identical.
On Windows 7 x64 with Scribus 1.4.5:
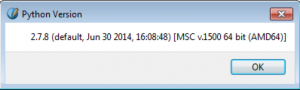
And with Scribus 1.5.0:
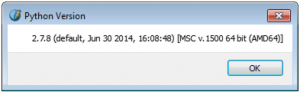
Looks like the Windows versions both embed the same version of Python.
It looks like I’ll need to install Ghostscript separately to enable some of the Scribus functionality relating to Postscript and EPS. I’ll look into that later.
Where are the scripts?
The second thing I want to know: where are the scripts? When you look at the Scribus Script (in 1.4.5) or Scripter (in 1.5.0) menu, it shows a whole range of sample scripts.
I’ll refer to the menu item as the Script menu item, even though it is called Scripter in 1.5.0. For example, when you see me mention a menu item Script – Show Console, it might actually be called Scripter – Show Console.
On the Mac, the scripts shown in the menu are located inside the Scribus app. On my system that’d be:
/Applications/Scribus.app/Contents/share/scribus/scripts
On Windows I found them here:
C:\Program Files\Scribus\share\scripts
This list of scripts shown in the menu seems to be refreshed only on restart of Scribus. If you add or modify any scripts while it’s running, the menu won’t update. This is unlike InDesign, where the Scripts Palette is dynamic and updates as scripts are added or modified.
Separate from that, there is also a configurable path to a scripts folder, which can be accessed via the Scribus – Preferences – Paths (in 1.5.0) or Scribus – Preferences – General (in 1.4.5) menu item.
This folder can be set to something like, say,
/Users/kris/Documents/Scribus Scripts
Somewhat surprising: this folder is only used when you use the Script – Execute Script… menu item: it is the default folder location your dialog will open to.
It does not affect the list of scripts shown in the Script menu; that folder location seems to be hard-coded.
How does the console work?
For my first test, I used the scribus.messageBox function to plunk something into a dialog. However, for debugging and so on, I’d love to get some continuous text output.
My next question is: how can I write to a console from a script?
There is a console under the Script – Show Console menu item, but that was not really what I was looking for.
It took me a bit of searching, and as it turns out, the secret to the Scribus Console window seems to be function key <F9>.
Enter or copy-paste a script in the top half of the Console, then press <F9>.
Depending on how your Mac is configured you might need to change the System Preferences, or possibly press <fn>-<F9> or something like that.
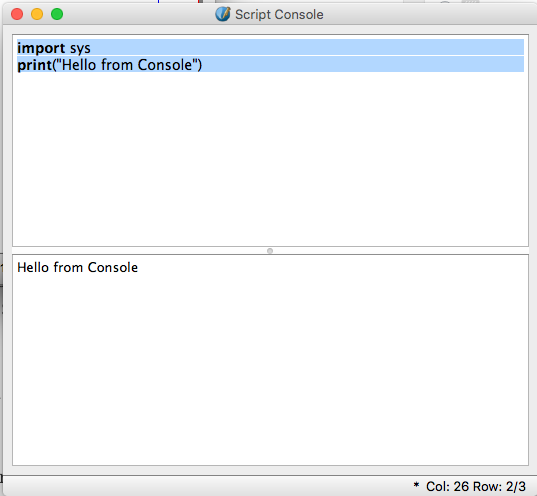
Check your System Preferences – Keyboard and System Preferences – Mission Control setup.
But that’s not really what I was after. I am looking for a way to get debugging info out from my scripts into a scrolling window.
The first method that worked for me was to start a Terminal window, and then navigate into the Scribus.app.
Then launch Scribus from the command line. After that, I get to see any output from Python in the Terminal window.
First I launch Scribus via the Terminal:
cd /Applications/Scribus.app/Contents/MacOS/
./Scribus
It spits out some information:
Path = /Applications/Scribus.app
"scpaths: bundle at /Applications/Scribus.app"
"scpaths: doc dir=/Applications/Scribus.app/Contents/share/doc/scribus/"
"scpaths: icon dir=/Applications/Scribus.app/Contents/share/scribus/icons/"
"scpaths: font dir=/Applications/Scribus.app/Contents/share/scribus/fonts/"
"scpaths: sample dir=/Applications/Scribus.app/Contents/share/scribus/samples/"
"scpaths: script dir=/Applications/Scribus.app/Contents/share/scribus/scripts/"
"scpaths: template dir=/Applications/Scribus.app/Contents/share/scribus/templates/"
"scpaths: lib dir=/Applications/Scribus.app/Contents/lib/"
"scpaths: plugin dir=/Applications/Scribus.app/Contents/lib/"
"scpaths: QML dir=/Applications/Scribus.app/Contents/share/scribus/qml/"
"scpaths: qtplugins=/Applications/Scribus.app/Contents/PlugIns:/Applications/Scribus.app/Contents/MacOS"
Fontconfig error: Cannot load default config file
Then I run a little ‘Hello World’ Python script via the Script -Execute Script… menu item.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import sys
print "Hello World"
That makes ‘Hello World’ appear in my terminal window.
Another way that works is to use the Python syslog. The script
import syslog
syslog.syslog(syslog.LOG_ALERT, 'Hello in syslog')
makes a log entry appear in the /var/log/system.log file.
What about the scribus module
I started Scribus from the command line as shown before, and then ran the following script:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import scribus
help(scribus)
That made it spit out oodles of documentation in the Terminal window.
You can also simply type
help(scribus)
into the Console window, then hit <F9>.
To come
Here’s a bunch of stuff I still want to look into:
Scribus console mode
C++ plug-ins:
http://wiki.scribus.net/canvas/Plugin_Architecture
C++ API
http://wiki.scribus.net/canvas/Public_C%2B%2B_API
Extension Scripts vs. regular scripts?
UTF-8 and stuff? How does it handle file names with non-ASCII characters? And text with non-ASCII characters?
Database publishing. Maybe tie a FileMaker and/or MySQL database to Scribus, just to try it out?